基于统计的分词方法

1.n元语言模型(n-gram)

假设$S$表示长度为$i$，由$(w_1,w_2,\dots,w_m)$字序列组成的句子，则代表$S$的概率为：

$$ P(S) = P(w_1,w_2,\dots,w_m) = P(w_1)*P(w_2|w_1)*P(w_3|w_2,w_1)\cdots P(w_i|w_1,w_2,\dots,w_{m-1}) $$

$$ P(w_1,w_2,\dots,w_m) =\prod_{i=1}^mP(w_i) $$

$$ P(w_1,w_2,\dots,w_m) =\prod_{i=1}^mP(w_i|w_{i-1}) $$

$$ P(w_1,w_2,\dots,w_m) =\prod_{i=1}^mP(w_i|w_{i-2}w_{i-1}) $$

HMM的参数

观测序列(输出状态序列),状态序列(隐藏状态序列),初始概率,转移概率(转移概率矩阵),发射概率(发射概率矩阵)

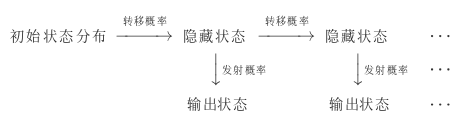
数学定义

状态值集合(隐藏状态):$Q={q_1,q_2,\cdots,q_N}$,$N$为可能的状态数,对应状态序列$I$

观测值集合(输出状态):$V={v_1,v_2,\cdots,v_M}$,$M$为可能的观测数,对应观测序列$O$

转移概率矩阵:$A=[a*{ij}];i,j\in{1,2,\cdots,N}$,从$i$状态到$j$状态的转换概率($\sum*{j=1}^Na_{ij}=1$)

发射概率矩阵(观测概率矩阵):$B=[b_j(k)];j\in{1,2,\cdots,N},k\in{1,2,\cdots,M}$,从状态$j$生成观测$k$的概率

初始状态分布:$\pi$

模型:$\lambda=(A,B,\lambda)$,状态序列$I$,观测序列$O$

HMM中的三个问题:

HMM是一种序列模型,不仅可以用到自然语言处理这个领域,其他领域的应用也很常见:股指预测,语音识别,网络安全,基因序列等方面

在自然语言处理中,HMM可以应用在分词,词性标注,命名实体识别等各个方面.

在分词方面可以这样理解HMM

观测序列(输出状态序列)----序列构成的句子或短文

状态序列(隐藏状态序列)----标注

初始概率----统计的第一个字序的概率

转移概率(转移概率矩阵)----第$i$个字序到第$i+1$个自序的标注变换概率

发射概率(发射概率矩阵)----从隐藏状态到输出状态的转换概率

如果把观测序列看作标注,状态序列看作句子,从解码问题转变成学习问题会怎样

在序列预测问题中

HMM模型:当前tag仅依赖前一个tag,当前输出仅依赖当前tag(文档的单词序列是由隐藏状态的标签决定的)

MEMM(最大熵马尔科夫模型)模型:当前tag取决于观察值x(单词)和前一个tag(序列的标签取决于前一个标签和当前的单词)

CRF模型:计算损失时把一句话看作一个整体计算损失