SNR与EVM的关系
关系
当SNR较大(大于10dB)时,SNR=-20lg(EVM),其中SNR的单位为dB,EVM为正实数。
如果EVM用dB表示,可以简化为SNR = -2*EVM_dB。(此式在SNR大于4dB时,误差较小,不超过1dB)
下面依次介绍 log、dB、dBm、evm、snr的概念,再说明此结论的推导过程。
对数公式
如果a^b=N(a>0,且a≠1,则b叫做以a为底N的对数,公式如下,其中a叫做底数,N叫做真数, b叫对数。
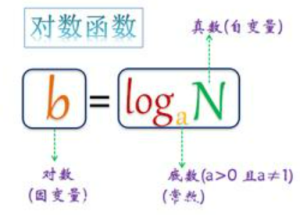
通常我们将以10为底的对数叫常用对数,以e为底的对数叫自然对数。
常用对数:$ lg(b) = log_{10}(b) $ (10为底数)。
自然对数:$ ln(b) = log_{e}(b) $ (e为对数)。
对数的基本性质中,下面的结论经常用到:
$$ \begin{array}{l} log_{a}M^n = nlog_{a}M \cr lg10 = 1 \cr lg2 \approx 0.3 \cr lg1 = 0 \end{array} $$
信号强度
日常中通常使用功率来衡量一个电器做功的快慢,如一个10W的电灯泡,10W功率就是电灯泡消耗能量做功的快慢。
在天线收发系统里,同样也需要消耗电能来转换为电磁波的能量进行传输。
但是电磁波的能量衰减非常快,例如一个100mW的能量源,传输一段距离后很快就能衰减成1mW、0.1mW、0.01mW甚至更小。
对于这种呈几何数量级的衰减,使用功率来衡量会给计数带来不便,因此引用新的概念:dB和dBm。
dB介绍
dB是一个表征相对值的值,纯粹的比值,只表示两个量的相对大小关系,没有单位。公式为dB=10lg(A/B),一般作为(SNR)信噪比、损耗的单位。
当考虑甲的功率相比于乙功率大或小多少个dB时,按下面的计算公式:10log(甲功率/乙功率)。
例如A的功率为100mW,B的功率为10mW,则10lg(100 / 10) = 10dB,说明A比B大10dB。
例:如何理解:+3 dB表示增大为两倍,-3 dB表示下降为1/2。 如果A的功率开始为100mW,经过衰减变成了50mw,则10lg(50 / 100) = 10lg(1/ 2) = -10lg(2)= -3dB。 如果A的功率开始为100mW,经过放大变成了200mw,则10lg(200 / 100) = 10lg(2) = 3dB。
dBm介绍
dBm是一个表示功率绝对值(可以认为是以1mW功率为基准的一个比值),计算公式为:10log(功率值/1mw)。
记住一个口诀: 加3乘2, 加10乘10; 减3除2,减10除10 (+3 dB,表示功率增加为2倍;+10 dB,表示功率增加为10倍。-3 dB,表示功率减小为1/2;-10 dB,表示功率减小为1/10)。
例:功率P为1mw,折算为dBm后为0dBm。 40W的功率,按dBm单位进行折算后的值应为: 10log(40W/1mw)=10log(40000)= 46dBm。 按口决: 40W = 1w * (( 10 * 10 * 10)W * 10 * 2 * 2) => 10 + 10 + 10 + 10 + 3 + 3 = 46dBm 那么44dBm 是多少W? (25W)
需要注意的是,对于功率的增益,我们用10lg(Po/Pi),而对于电压和电流的增益,要用20lg(Vo/Vi)、20lg(Io/Ii)。
原因是 这个2来源于电功率转换公式的平方上:
$$ P = UI = I^2R = \frac {U^2} {R} $$
SNR和EVM
SNR介绍
信噪比SNR(Signal-to-noise Ratio),指的是系统中信号与噪声的比。公式为 SNR = 10lg(Ps / Pn),其中:
- SNR:信噪比,单位是dB。
- Ps:信号的有效功率。
- Pn:噪声的有效功率。
$$ SNR(dB) = 10 *lg \frac {\int s(t)^2 \mathrm{d}t} {\int n(t)^2 \mathrm{d}t} = 10 * lg \frac {\int s(t)^2 \mathrm{d}t} {\int (x(t)-s(t))^2 \mathrm{d}t}\tag{1} $$
式中$ x(t) $ 为矢量reference signal,$ s(t) $ 为矢量输入信号。
EVM介绍
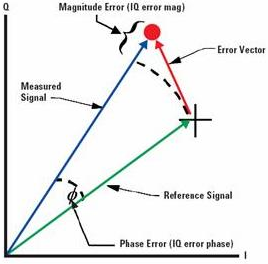
QAM 调制信号通常用其EVM 来衡量信号质量,EVM是英文Error Vector Magnitude缩写,意为误差向量幅度。
误差矢量Error Vector 的幅度与参考信号Reference Signal 幅度的比值。通常测量的EVM为其RMS 值(Root Mean Square均方根),计算公式如:
$$ EVM=\sqrt {\frac {\int (x(t)-s(t))^2 \mathrm{d}t} {\int x(t)^2 \mathrm{d}t}}\tag{2} $$
式中$ x(t) $ 为矢量reference signal,$ s(t) $ 为矢量输入信号。
大多时候,EVM用dB表示:
$$ EVM_{dB} = 10*lg{EVM} $$
SNR与EVM关系
从(1)式 和(2)式可以看出:当矢量输入信号$ s(t) $越接近于矢量reference signal $ x(t) $,即$ s(t) $可以用$ x(t) $代替,推导如下:
$$ \begin{array}{l} SNR(dB) = 10 * lg \frac {\int s(t)^2 \mathrm{d}t} {\int (x(t)-s(t))^2 \mathrm{d}t} \cr \approx 10 * lg \frac {\int x(t)^2 \mathrm{d}t} {\int (x(t)-s(t))^2 \mathrm{d}t} \cr = -1 * 10 * lg \frac {\int (x(t)-s(t))^2 \mathrm{d}t} {\int x(t)^2 \mathrm{d}t} \cr = -10 * lg({EVM}^2) \cr =-2 * 10 * lg(EVM) =-2EVM_{dB} \end{array} $$